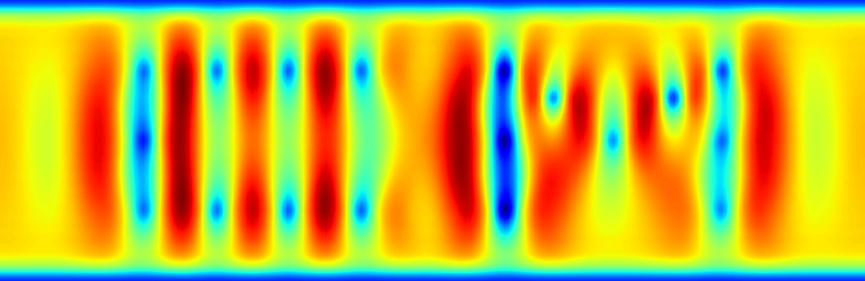
FSDT - First-order Shear Deformation Theory¶
Description¶
For the FSDT the displacement field components are:
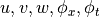
The displacement field is approximated similarly to the
CLPT, but here  and
and  are independent variables, relaxing the approximation.
are independent variables, relaxing the approximation.
For the ConeCyl implementations, the approximation functions are
separated into three components:
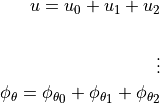
where  contains the approximation functions corresponding to the
prescribed degrees of freedom,
contains the approximation functions corresponding to the
prescribed degrees of freedom, 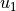 contains the functions independent
of
contains the functions independent
of  and
and  the functions that depend on both
the functions that depend on both 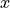 and
and  .
.
The aim is to have a model capable to simulate non-rigid supports, and where
the displacement components 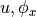 can habe a non-costant value
along the edges.
can habe a non-costant value
along the edges.
It is of special importance to allow  to be between zero
(clamped) and another value (up to simply supported),
by using elastic stiffnesses for the corresponding degrees of freedom. The
elastic stiffnesses are implemented for the FSDT in the same manner described
for the CLPT.
to be between zero
(clamped) and another value (up to simply supported),
by using elastic stiffnesses for the corresponding degrees of freedom. The
elastic stiffnesses are implemented for the FSDT in the same manner described
for the CLPT.
Models¶
The recommended models, according to the desired boundary condition , are:
SS1- or CC1-type: fsdt_donnell_bc1
SS2- or CC2-type: fsdt_donnell_bc2
SS3- or CC3-type: fsdt_donnell_bc3
SS4- or CC4-type: fsdt_donnell_bc4
Note that the fsdt_donnell_bc4 model can be used to simulate all the other types of boundary condition, which is allowed by the use of elastic constraints.
A more general model, the fsdt_donnell_bcn (or the counterpart
fsdt_sanders_bcn) has been proposed and despite it has the largest
simulation capabilities, it can be unstable for high stiffeness applied
to the elastic constraints. Moreover, this model cannot simulate the linear
buckling analysis of the  type of boundary conditions.
type of boundary conditions.
The models below were kept for future reference only and have been used in comparative studies:
fsdt_donnell_bc1¶
SS1- and CC1-types of boundary conditions.
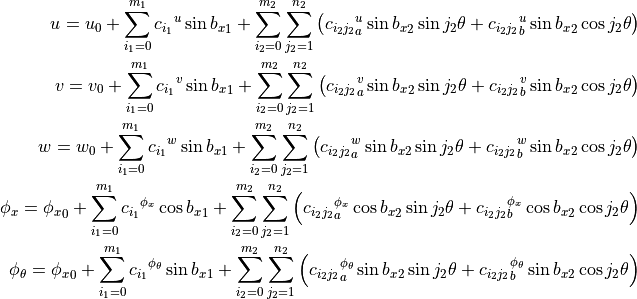
Observations:
linear static implemented
linear buckling implemented
non-linear analysis implemented
fsdt_donnell_bc2¶
SS2- and CC2-types of boundary conditions.

Observations:
linear static implemented
linear buckling implemented
non-linear analysis implemented
fsdt_donnell_bc3¶
SS3- and CC3-types of boundary conditions.
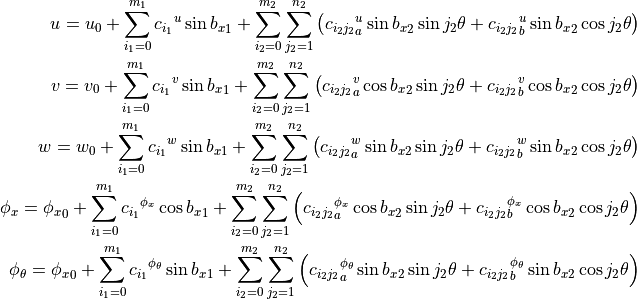
Observations:
linear static implemented
linear buckling implemented
non-linear analysis implemented
fsdt_donnell_bc4¶
SS4- and CC4-types of boundary conditions.

Observations:
linear static implemented
linear buckling implemented
non-linear analysis implemented
fsdt_donnell_bcn¶
The current attempt adds more flexibility in  .
The resulting approximation functions are:
.
The resulting approximation functions are:

Observations:
linear static implemented
linear buckling not working
non-linear analysis implemented
fsdt_sanders_bcn¶
Counterpart of fsdt_donnell_bcn using the Sanders non-linear equations.
Observations:
linear static implemented
linear buckling not working
non-linear analysis not implemented
fsdt_shadmehri2012_bc2¶
Note
NOT RECOMMENDED, implemented for comparative purposes only.
Adapted from the model published by Shadmehri (2012) ([shadmehri2012], [shadmehri2012thesis]) for the SS2- and CC2-types of boundary conditions. Uses the Donnell’s equations and the approximation functions are:

Observations:
linear buckling implemented
linear static not implemented
non-linear analysis not implemented
fsdt_shadmehri2012_bc3¶
Note
NOT RECOMMENDED, implemented for comparative purposes only.
Published by Shadmehri (2012) (see [shadmehri2012] or [shadmehri2012thesis] for more details). This model was developed to simulate the SS3- and CC3-types of boundary condition. Uses the Donnell’s equations and the approximation functions are:
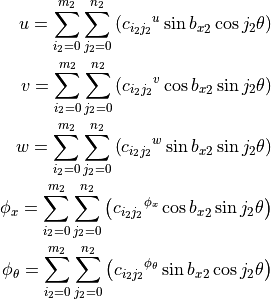
Observations:
linear buckling implemented
linear static not implemented
non-linear analysis not implemented
fsdt_geier1997_bc2¶
Note
NOT RECOMMENDED, implemented for comparative purposes only.
Published by Geier and Singh (1997) (see [geier1997] for more details). This model was developed to simulate the SS2- and CC2-types of boundary condition. Such models seem to be originally proposed by Khdeir et al. (1989) (see [khdeir1989]). Uses the Donnell’s equations and the approximation functions are:

Observations:
linear buckling implemented
linear static not implemented
non-linear analysis not implemented