Interpolate (compmech.interpolate)

This module includes some interpolation utilities that will be used in other modules.

compmech.interpolate.inv_weighted(data, mesh, num_sub, col, ncp=5, power_parameter=2)[source]

Interpolates the values taken at one group of points into another using an inverse-weighted algorithm

In the inverse-weighted algorithm a number of 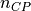n_{CP} measured points of the input parameter data that are closest to a given node in the input parameter mesh are found and the imperfection value of this node (represented by the normal displacement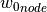 {w_0}_{node}) is calculated as follows: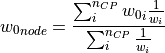

{w_0}_{node} = \frac{\sum_{i}^{n_{CP}}{{w_0}_i\frac{1}{w_i}}} {\sum_{i}^{n_{CP}}{\frac{1}{w_i}}}

where 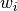w_i is the imperfection at each measured point, calculated as:

w_i = \left[(x_{node}-x_i)^2+(y_{node}-y_i)^2+(z_{node}-y_i)^2 \right]^p

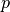with p being a power parameter that when increased will increase the relative influence of a closest point.

Parameters
datanumpy.ndarray, shape (N, ndim+1)

The data or an array containing the imperfection file. The values to be interpolated must be in the last column.

meshnumpy.ndarray, shape (M, ndim)

The new coordinates where the values will be interpolated to.

num_subint

The number of sub-sets used during the interpolation. The points are divided in sub-sets to increase the algorithm’s efficiency.

colint

The index of the column to be used in order to divide the data in sub-sets. Note that the first column index is 0.

ncpint, optional

Number of closest points used in the inverse-weighted interpolation.

power_parameterfloat, optional

Power of inverse weighted interpolation function.

Returns
ansnumpy.ndarray

A 1-D array with the interpolated values. The size of this array is mesh.shape[0].

compmech.interpolate.interp(x, xp, fp, left=None, right=None, period=None)[source]

One-dimensional linear interpolation

Returns the one-dimensional piecewise linear interpolant to a function with given values at discrete data-points.

Note

This function has been incorporated in NumPy >= 1.10.0 and will be soon removed from here.

Parameters
xarray_like

The x-coordinates of the interpolated values.

xp1-D sequence of floats

The x-coordinates of the data points, must be increasing if argument period is not specified. Otherwise, xp is internally sorted after normalizing the periodic boundaries with xp = xp % period.

fp1-D sequence of floats

The y-coordinates of the data points, same length as xp.

leftfloat, optional

Value to return for x < xp[0], default is fp[0].

rightfloat, optional

Value to return for x > xp[-1], default is fp[-1].

periodfloat, optional

A period for the x-coordinates. This parameter allows the proper interpolation of angular x-coordinates. Parameters left and right are ignored if period is specified.

Returns
y{float, ndarray}

The interpolated values, same shape as x.

Raises
ValueError

If xp and fp have different length If xp or fp are not 1-D sequences If period==0

Notes

Does not check that the x-coordinate sequence xp is increasing. If xp is not increasing, the results are nonsense. A simple check for increasing is:

np.all(np.diff(xp) > 0)

Examples

>>> xp = [1, 2, 3]
>>> fp = [3, 2, 0]
>>> interp(2.5, xp, fp)
1.0
>>> interp([0, 1, 1.5, 2.72, 3.14], xp, fp)
array([ 3. ,  3. ,  2.5 ,  0.56,  0. ])
>>> UNDEF = -99.0
>>> interp(3.14, xp, fp, right=UNDEF)
-99.0

Plot an interpolant to the sine function:

>>> x = np.linspace(0, 2*np.pi, 10)
>>> y = np.sin(x)
>>> xvals = np.linspace(0, 2*np.pi, 50)
>>> yinterp = interp(xvals, x, y)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.plot(xvals, yinterp, '-x')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()

Interpolation with periodic x-coordinates:

>>> x = [-180, -170, -185, 185, -10, -5, 0, 365]
>>> xp = [190, -190, 350, -350]
>>> fp = [5, 10, 3, 4]
>>> interp(x, xp, fp, period=360)
array([7.5, 5., 8.75, 6.25, 3., 3.25, 3.5, 3.75])